WSL中安装Docker

剑指offer中的一道题：

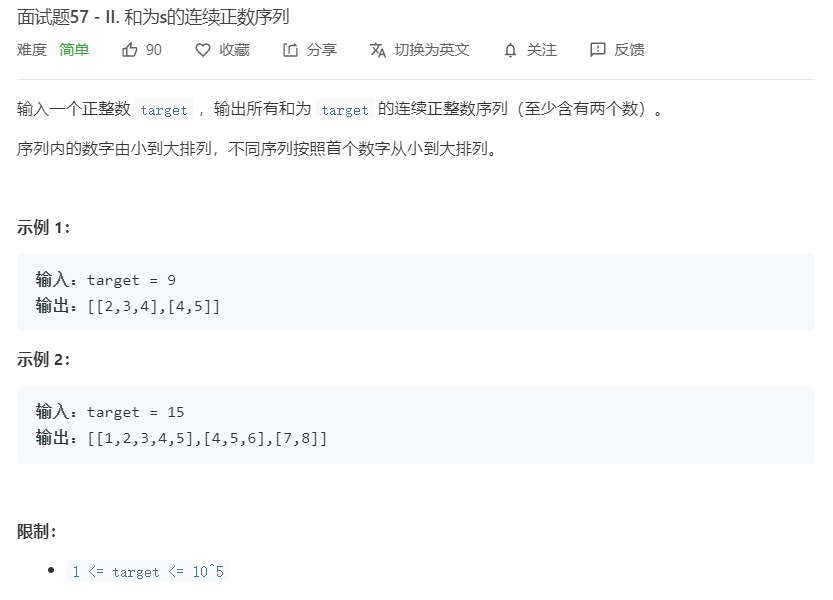
一般解法也就考虑到滑动窗口什么的，但在评论区里发现了一个双百的新解法：

public int[][] findContinuousSequence(int target) {

    List<int[]> result = new ArrayList<>();
    int i = 1;

    while(target>0)
    {
        target -= i++;
        if(target>0 && target%i == 0)
        {

            int[] array = new int[i];
            for(int k = target/i, j = 0; k < target/i+i; k++,j++)
            {
                array[j] = k;
            }
            result.add(array);
        }
    }
    Collections.reverse(result);
    return result.toArray(new int[0][]);
}

初看一脸懵，细思则大有门道。思路为 数学优化+枚举

我们先由题意可得等式：

x + (x+1) + (x+2) + ... + (x+i-1) = target;
//等价于
ix + i(i-1)/2 = target;
//等价于
x = (2target + i - i^2) / 2i = target/i + (1-i)/2;

即起始整数为 x 的连续 i 个整数相加，等于 target 。

所以我们只要挨个试 i ，找到符合的 x 就可以获得相关序列；

¶如何找到符合条件的 i ？

由等式：

x + (x+1) + (x+2) + ... + (x+i-1) = target;

可得

ix = target - ( 0 + 1 + 2 +...+ i-1 )

所以要找是否有连续 i 个整数的序列符合条件，我们只要判断 (target - （0+1+…+i-1)) % i == 0

所以有：

while(target>0)
{
    target -= i++;
    if(target>0 && target%i == 0)
    {
        //...
    }
}

然后我们就确定这连续 i 个整数的起始数：用已减去( 0 + 1 + 2 +…+ i-1 )的新target值除以 i 就能得到。随后的数字由起始数累加就能得到了。

while(target>0)
{
    target -= i++;
    if(target>0 && target%i == 0)
    {
        int[] array = new int[i];
        for(int k = target/i, j = 0; k < target/i+i; k++,j++)
        {
            array[j] = k;
        }
        result.add(array);
    }
}

最后再次佩服想出此解法的数学小机灵。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，邮件至 708801794@qq.com