WSL中安装Docker

剑指offer42：连续子数组的最大和

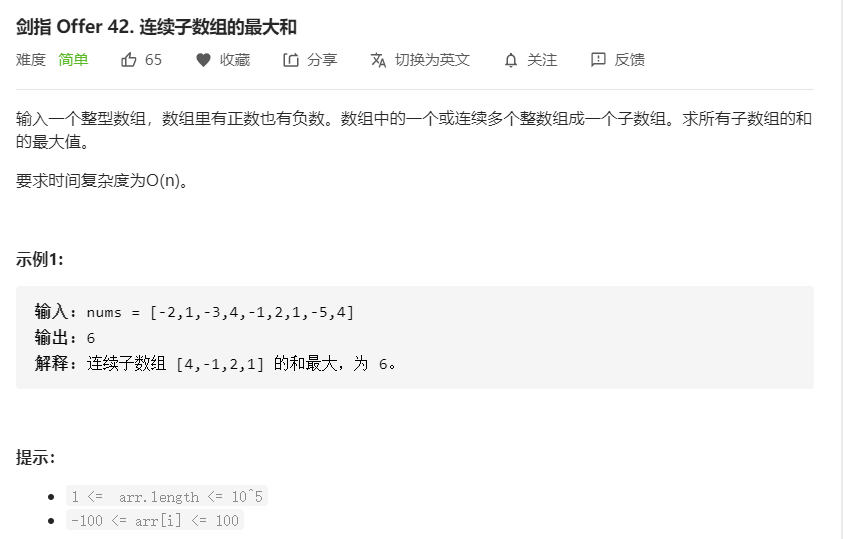
链接：https://leetcode-cn.com/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof/

解法：动态规划

class Solution {
    /**
     * 遍历数组中每一个数字，
     * 若当前索引的前一个数字为正数，将它累加到当前索引指向的数字中
     * 若当前索引的前一个数字不为正数，就不累加了
     * 每一步都将当前索引指向的值与已有最大值比较。
     */
    public int maxSubArray(int[] nums) {
        int maxSum = nums[0];
        for(int i = 1 ; i < nums.length ; i++){
            nums[i] += Math.max(nums[i-1], 0);
            maxSum = Math.max(maxSum, nums[i]);
        }
        return maxSum;
    }
}

从索引1开始，将前一个索引的值累加到当前索引，除非前一个索引值是负的，导致累加到当前索引后当前索引值比原来要小，还不如不加它。

每次遍历一个索引后，都将当前索引值与历史最大值比较，若比既有最大值还大，那么该值成为新的最大值。

反推，理解该算法：

对于和最大的连续子数组（设起点索引为 x 终点索引为 y ），前面的任意连续子数组（前面任意索引 到 x-1）都是负资产（负数），后面的连续任意子数组（y+1 到 后面任意索引）也是负资产。

所以我从其前面无论哪个索引出发开始累加，累加到 x-1 时都是非正数，此时我不再将这段累加结果再累加到 x 上。也就是说，这种做法使我一定能抛弃掉 x 前的任何负资产，找到 x 。

我从 x 开始新的一轮累加，每一次都与已有最大值作比较，所以遍历累加到 y 出现新的最大值时我一定能记录得到。此后再累加多少负资产也没所谓，因为我已经在遍历到 y 时记录到最大值了。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达，邮件至 708801794@qq.com